Notes about FARGO MPI implementation


The MPI implementation of a hydrocode usually consists in splitting the mesh in a number of submeshes equal to the number of processing elements (processors). Each processor can only access its own submesh, and has to communicate with its "neighbours" so as to set the hydrodynamic variables in its ghost zones. The MPI implementation of FARGO obeys this general picture, but it is subject to an important restriction: normally, it is a good idea to split the mesh in Nx*Ny submeshes (with Nx*Ny=number of CPUs), in such a way that Nx and Ny are proportionnal to the number of zones respectively in x and y. This ensures that the amount of communications between processors will be as small as possible. For instance, the figure below shows how the mesh was split on a 12-processor run of the code JUPITER for one of the test problems of the EU hydrocode comparison:
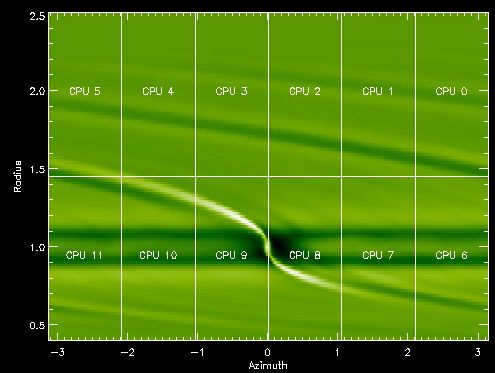jupiter mesh subdivision example

We see that the mesh is split both in azimuth and radius. Such a splitting is not possible with FARGO. Indeed, the FARGO algorithm implies azimuthal displacement of material of several zones over one timestep. If the mesh were split in azimuth, the communication between two processors could be very expensive (and tricky to implement), as one of them (the upstream one) should send many zone layers to the downstream one. 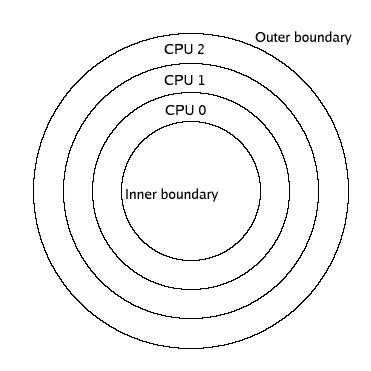For this reason, in the MPI implementation of FARGO, the mesh is exclusively split radially, in a number of  rings equal to the number of processors, as depicted below.
FARGO mesh splitting example

The implementation of such a splitting is obviously very simple, but not as efficient as a radial and azimuthal splitting. The amount of communication is not optimal. Furthermore, since only one communication is performed per hydrodynamical timestep, the number of zone layers that one processor needs to send to its neighbors is equal to 5 (4 for a standard ZEUS-like scheme, plus one for the viscous stress), which is a relatively large number (larger for instance than in the Godunov method code JUPITER, where the communication layers are only 2 zone wide).
One should therefore remember that the MPI implementation of FARGO, owing to the very nature of the FARGO algorithm and the adopted numerical scheme, is not very performant, and that one will only get a good scaling for a large number of zones radially. This should not be a problem anyway since FARGO is very fast even on a sequential platform, so one will need to run it on a parallel platform only at very large resolution, in which case the speed scaling provided by MPI will be satisfactory.
We conclude this section with two remarks about runtime details:

  1. if one runs the parallel version on several processors without using the flag -m (merge), every processor dumps its data in a separate file. Such output cannot be read with the IDL widget provided, for instance.  Assume we are considering the gas surface density data at output number 100. A sequential run would provide only one file, with name 'gasdens100.dat'. A parallel run on say, 4 processors, will provide the following four files: 'gasdens100.dat', 'gasdens100.dat.00001', 'gasdens100.dat.00002' and 'gasdens100.dat.00003'. They correspond to rings of increasing radius, so that simply concatenating these files will result in the file 'gasdens100.dat' of a sequential run:
    cat gasdens100.dat.* >> gasdens100.dat
    However, instead of doing this manually for each timestep, you can just run FARGO with the '-m' flag. This does the same thing automatically:
    mpirun -np 5 ./fargo -m in/inputfile.par
  2. Some parts of the hydrodynamical timestep in FARGO involve integrals (sums) of quantities over the mesh (such as the mass and angular momentum monitoring, or the torque evaluation onto the planet(s)). By default, each processor performs its own partial sum and at the end these partial results are combined to give the total sum. The result may not be equal to the sum of exactly the same quantity by one processor only, owing to machine precision issues. Although the difference is extremely small and should not be a worry, it might be sometimes desirable to get exactly the same result (mainly for debugging purposes, e.g. if you add a module and want to test if its MPI implementation is correct). In order to impose to FARGO to perform those sums exactly as one processor, use the -z flag (fake sequential). Note however that the -z flag does not work for an accreting planet (the update of the planet mass and angular momentum involve sums within the Roche lobe). If you have accreting planets, you might notice some difference between a parallel run with the -z flag and a sequential run if your planet is close to a boundary between two CPUs and accretes material from these two CPUs.